백준 7562번 나이트의 이동: C언어 풀이

백준 7562 나이트의 이동 문제의 C언어 해설입니다.
일반적인 BFS 구현에서 시작해, 체스판 크기를 조작해 실행 시간을 최적화 하는 과정을 단계적으로 설명합니다.

기본 접근: BFS를 이용한 나이트의 이동 구현

나이트의 처음 시작 포지션을 큐에 넣는다. 움직일 수 있는 8가지 경우의 수에 대해 BFS를 돌려준다.
목표 지점에 도달하기까지의 소요 시간은 매 iteration 마다 큐의 크기 만큼만 pop 하는 것으로 계산할 수 있다.

구현 코드

#include <stdio.h>

#define MAX_BOARD_SIZE 300
#define VISITED 1

struct position
{
    short row, col;
};

struct board
{
    int cells[MAX_BOARD_SIZE][MAX_BOARD_SIZE];
    int size;
    struct position start, target;
    struct position queue[MAX_BOARD_SIZE * MAX_BOARD_SIZE];
    int q_head, q_tail;
};

/* Board Macros */
#define IS_SAME_CELL(x, y) ((x).row == (y).row && (x).col == (y).col)
#define IS_WITHIN_BOARD(x, size) ((x).row >= 0 && (x).row < (size) && (x).col >= 0 && (x).col < (size))
#define CELL(boardp, pos) ((boardp)->cells[(pos).row][(pos).col])

/* Board Queue Macros */ 
#define Q_POP(boardp) ((boardp)->queue[(boardp)->q_head++])
#define Q_PUSH(boardp, pos) ((boardp)->queue[(boardp)->q_tail++] = (pos))
#define Q_SIZE(boardp) ((boardp)->q_tail - (boardp)->q_head)

int get_moves(struct board *board);
void clear_board(struct board *board);

int main(void)
{
    int num_cases;
    scanf("%d", &num_cases);

    struct board board;
    int num_moves;
    for (int i = 0; i < num_cases; i++)
    {
        scanf("%d", &(board.size));
        scanf("%hd %hd", &(board.start.row), &(board.start.col));
        scanf("%hd %hd", &(board.target.row), &(board.target.col));

        num_moves = get_moves(&board);
        printf("%d\n", num_moves);

        clear_board(&board);
    }
}

int get_moves(struct board *board)
{
    if (IS_SAME_CELL(board->start, board->target))
    {
        return 0;
    }

    /* Knight moves */
    int di[8] = {1, 2, 2, 1, -1, -2, -2, -1};
    int dj[8] = {2, 1, -1, -2, 2, 1, -1, -2};

    /* Init BFS */
    board->q_head = 0;
    board->q_tail = 0;
    Q_PUSH(board, board->start);
    CELL(board, board->start) = VISITED;

    int num_paths;
    struct position curr, next;
    for (int num_moves = 0; Q_SIZE(board) != 0; num_moves++)
    {
        num_paths = Q_SIZE(board);
        for (int p = 0; p < num_paths; p++)
        {
            curr = Q_POP(board);
            for (int dir = 0; dir < 8; dir++)
            {
                next.row = curr.row + di[dir];
                next.col = curr.col + dj[dir];
                if (IS_WITHIN_BOARD(next, board->size) && CELL(board, next) != VISITED)
                {
                    if (IS_SAME_CELL(next, board->target))
                    {
                        return num_moves + 1;
                    }
                    Q_PUSH(board, next);
                    CELL(board, next) = VISITED;
                }
            }
        }
    }
    return -1;
}

void clear_board(struct board *board)
{
    for (int i = 0; i < board->size; i++)
    {
        for (int j = 0; j < board->size; j++)
        {
            board->cells[i][j] = 0;
        }
    }
}

성능 최적화: 체스판 크기 자르기

앞선 코드는 비효율적인 움직임이 너무 많다.
체스 판 안에서 가능한 모든 움직임을 계산하기 때문이다.
특히 나이트가 목표 대상과 완전히 반대 방향으로 가는 것도 포함된다..

그렇다고 나이트가 목표 방향으로 이동하는 것만 고려할 수는 없다.
나이트의 특성 상 목표 지점에 정확히 도달하기 위해 뒤로 이동해야 하는 경우가 있기 때문이다.
효율을 위해서는 나이트가 목표 지점과 멀어지는 것을 필요한 만큼만 허용해야한다.

필요한 만큼만 멀어진다는 걸 계산할 지, 나름의 수학적인 해법이 있을 것 같기도 하지만 그건 좀 어렵다.
대신 목표 지점에 도달하기 위해 필요한 만큼 이동 공간을 제한하기로 한다.

필요한 이동 공간을 구하기 위해 다음과 같이 케이스를 나눠봤다.
대칭성을 고려해서 목표 위치는 나이트 기준 우상단 방향에 위치한다고 간주하자. (같은 열에 있는 것 포함)
나이트 기준 5x5 위치에 목적지가 있다고 가정하자. 아래 5 케이스로 나누어진다.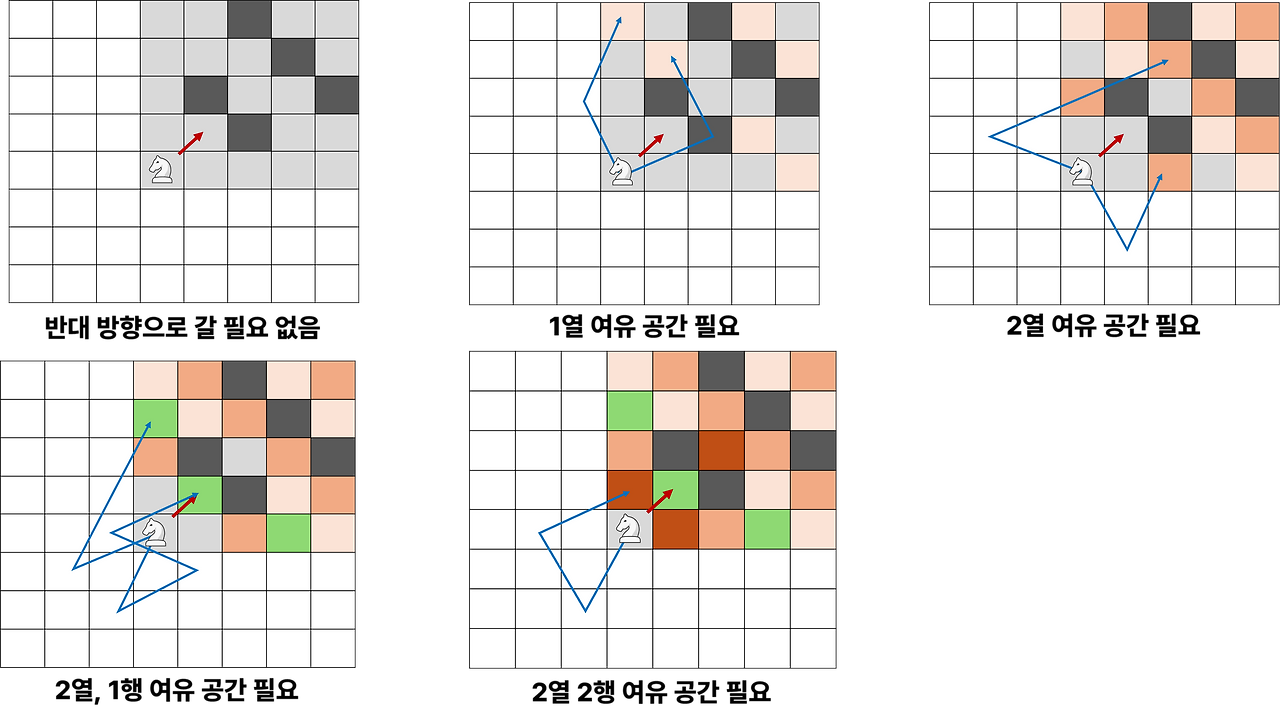

25개의 목적지만 고려했지만, 다른 모든 위치로도 확장 가능하다.
결국 목표 셀에 접근하기 위해서는 목표와 멀어지는 방향으로 이동하기 위한 최대 2x2 만큼의 여유 공간이 필요하다.
그 이상의 공간은 최소 이동을 도출하는 데 필요가 없다.

결론적으로 2x2의 여유 공간을 제외한 시작점과 끝점 바깥의 체스판의 나머지 공간은 죄다 잘라버려도 된다.

이를 위해 다음 함수를 정의해주었다.

void normalize_board(struct board *board)
{
    /* Flip board to make start point bottom-left (and target upper-right) */
    if (board->start.row > board->target.row)
    {
        board->start.row = (board->row_size - 1) - board->start.row;
        board->target.row = (board->row_size - 1) - board->target.row;
    }
    if (board->start.col > board->target.col)
    {
        board->start.col = (board->col_size - 1) - board->start.col;
        board->target.col = (board->col_size - 1) - board->target.col;
    }

    /* Cut the board to optimize BFS movement 
     * Knight might move backwards or past target to precisely reach target 
     * However, spaces more than 2 are not needed and thus capped at 2 */
    int left_padding = CAP_AT_TWO(board->start.row);
    int row_distance = board->target.row - board->start.row;
    int right_padding = CAP_AT_TWO((board->row_size - 1) - board->target.row);

    int down_padding = CAP_AT_TWO(board->start.col); 
    int col_distance = board->target.col - board->start.col;
    int up_padding = CAP_AT_TWO((board->col_size - 1) - board->target.col);

    board->start.row = left_padding;
    board->start.col = down_padding;
    board->target.row = board->start.row + row_distance;
    board->target.col = board->start.col + col_distance;
    board->row_size = board->target.row + right_padding + 1;
    board->col_size = board->target.col + up_padding + 1;
}

먼저 계산의 편의성을 위해 대칭 이동으로 시작점을 왼쪽 밑, 도착점을 우측 상단 점으로 만들어준다.
이후 시작점 기준 좌측과 하단의 남은 공간을 2칸만 남기고 죄다 잘라준다. (2칸보다 적을 시 그냥 둔다)
도착점의 우측과 상단 공간도 마찬가지로 진행한다.

이 때 정사각형이던 체스판이 직사각형이 된다. 따라서 row_size와 col_size 두 크기가 필요하다.

최적화된 구현 코드

#include <stdio.h>

#define MAX_BOARD_SIZE 300
#define VISITED 'V'

struct position
{
    short row, col;
};

struct board
{
    char cells[MAX_BOARD_SIZE][MAX_BOARD_SIZE];
    short row_size, col_size;
    struct position start, target;
    struct position queue[MAX_BOARD_SIZE * MAX_BOARD_SIZE];
    int q_head, q_tail;
};

/* Board Manipulation */ 
#define CAP_AT_TWO(x) ((x) >= 2 ? 2 : (x))

/* Board Macros */
#define IS_SAME_CELL(x, y) ((x).row == (y).row && (x).col == (y).col)
#define IS_WITHIN_BOARD(boardp, x) ((x).row >= 0 && (x).row < (boardp)->row_size && (x).col >= 0 && (x).col < (boardp)->col_size)
#define CELL(boardp, pos) ((boardp)->cells[(pos).row][(pos).col])

/* Board Queue Macros */ 
#define Q_POP(boardp) ((boardp)->queue[(boardp)->q_head++])
#define Q_PUSH(boardp, pos) ((boardp)->queue[(boardp)->q_tail++] = (pos))
#define Q_SIZE(boardp) ((boardp)->q_tail - (boardp)->q_head)

void normalize_board(struct board *board);
int get_moves(struct board *board);
void clear_board(struct board *board);

int main(void)
{
    int num_cases;
    scanf("%d", &num_cases);

    struct board board;
    int num_moves;
    for (int i = 0; i < num_cases; i++)
    {
        scanf("%hd", &(board.row_size));
        board.col_size = board.row_size;
        scanf("%hd %hd", &(board.start.row), &(board.start.col));
        scanf("%hd %hd", &(board.target.row), &(board.target.col));

        normalize_board(&board);
        num_moves = get_moves(&board);
        printf("%d\n", num_moves);

        clear_board(&board);
    }
}

void normalize_board(struct board *board)
{
    /* Flip board to make start point bottom-left (and target upper-right) */
    if (board->start.row > board->target.row)
    {
        board->start.row = (board->row_size - 1) - board->start.row;
        board->target.row = (board->row_size - 1) - board->target.row;
    }
    if (board->start.col > board->target.col)
    {
        board->start.col = (board->col_size - 1) - board->start.col;
        board->target.col = (board->col_size - 1) - board->target.col;
    }

    /* Cut the board to optimize BFS movement 
     * Knight might move backwards or past target to precisely reach target 
     * However, spaces more than 2 are not needed and thus capped at 2 */
    int left_padding = CAP_AT_TWO(board->start.row);
    int row_distance = board->target.row - board->start.row;
    int right_padding = CAP_AT_TWO((board->row_size - 1) - board->target.row);

    int down_padding = CAP_AT_TWO(board->start.col); 
    int col_distance = board->target.col - board->start.col;
    int up_padding = CAP_AT_TWO((board->col_size - 1) - board->target.col);

    board->start.row = left_padding;
    board->start.col = down_padding;
    board->target.row = board->start.row + row_distance;
    board->target.col = board->start.col + col_distance;
    board->row_size = board->target.row + right_padding + 1;
    board->col_size = board->target.col + up_padding + 1;
}

int get_moves(struct board *board)
{
    if (IS_SAME_CELL(board->start, board->target))
    {
        return 0;
    }

    /* Knight moves */
    short di[8] = {1, 2, 2, 1, -1, -2, -2, -1};
    short dj[8] = {2, 1, -1, -2, 2, 1, -1, -2};

    /* Init BFS */
    board->q_head = 0;
    board->q_tail = 0;
    Q_PUSH(board, board->start);
    CELL(board, board->start) = VISITED;

    int num_paths;
    struct position curr, next;
    for (int num_moves = 0; Q_SIZE(board) != 0; num_moves++)
    {
        num_paths = Q_SIZE(board);
        for (int p = 0; p < num_paths; p++)
        {
            curr = Q_POP(board);
            for (short dir = 0; dir < 8; dir++)
            {
                next.row = curr.row + di[dir];
                next.col = curr.col + dj[dir];
                if (IS_WITHIN_BOARD(board, next) && CELL(board, next) != VISITED)
                {
                    if (IS_SAME_CELL(next, board->target))
                    {
                        return num_moves + 1;
                    }
                    Q_PUSH(board, next);
                    CELL(board, next) = VISITED;
                }
            }
        }
    }
    return -1;
}

void clear_board(struct board *board)
{
    for (int i = 0; i < board->row_size; i++)
    {
        for (int j = 0; j < board->col_size; j++)
        {
            board->cells[i][j] = 0;
        }
    }
}

1차 및 2차 성능 비교

BOJ 제출 결과 기준

1차: 1696 KB / 16ms

2차: 1436 KB / 4ms